
Dneska bych si chtěl hrát se souřadnicemi!
Tak tedy ano. Dnes si ukážeme něco málo práce, kdy budeme pracovat s různými souřadnými systémy. Hlavně ekliptikálními (ekliptikální délka l a šířka b), rovníkovými 2. druhu (rektascenze a a deklinace d) a obzorníkovými (azimut A a výška nad obzorem h).
Ale nebude to jen o tomto. Takže pozor, řešíme rovnou úlohy. Minule jsme vyřešili šest příkladů, tedy
7. Změřte výšku Vegy dne 9.5. 2021 ve 20 hodin letního času. Nyní určete, v kolik hodin bude o tento úhel na východ před kulminací
Pro tento úkol musíme nejprve nacvičit zaměření hvězdy. Astroláb otočíme na zadní stranu, zavěsíme jej za očko a takto pomocí záměrných hran alhidády zaměříme hvězdu, v tomto případě Vegu ze souhvězdí Lyry. Pokud budeme měřit dobře, musíme být mezi 10 ° a 11°. Takže zadní deka by měla být po měření v tomto stavu:
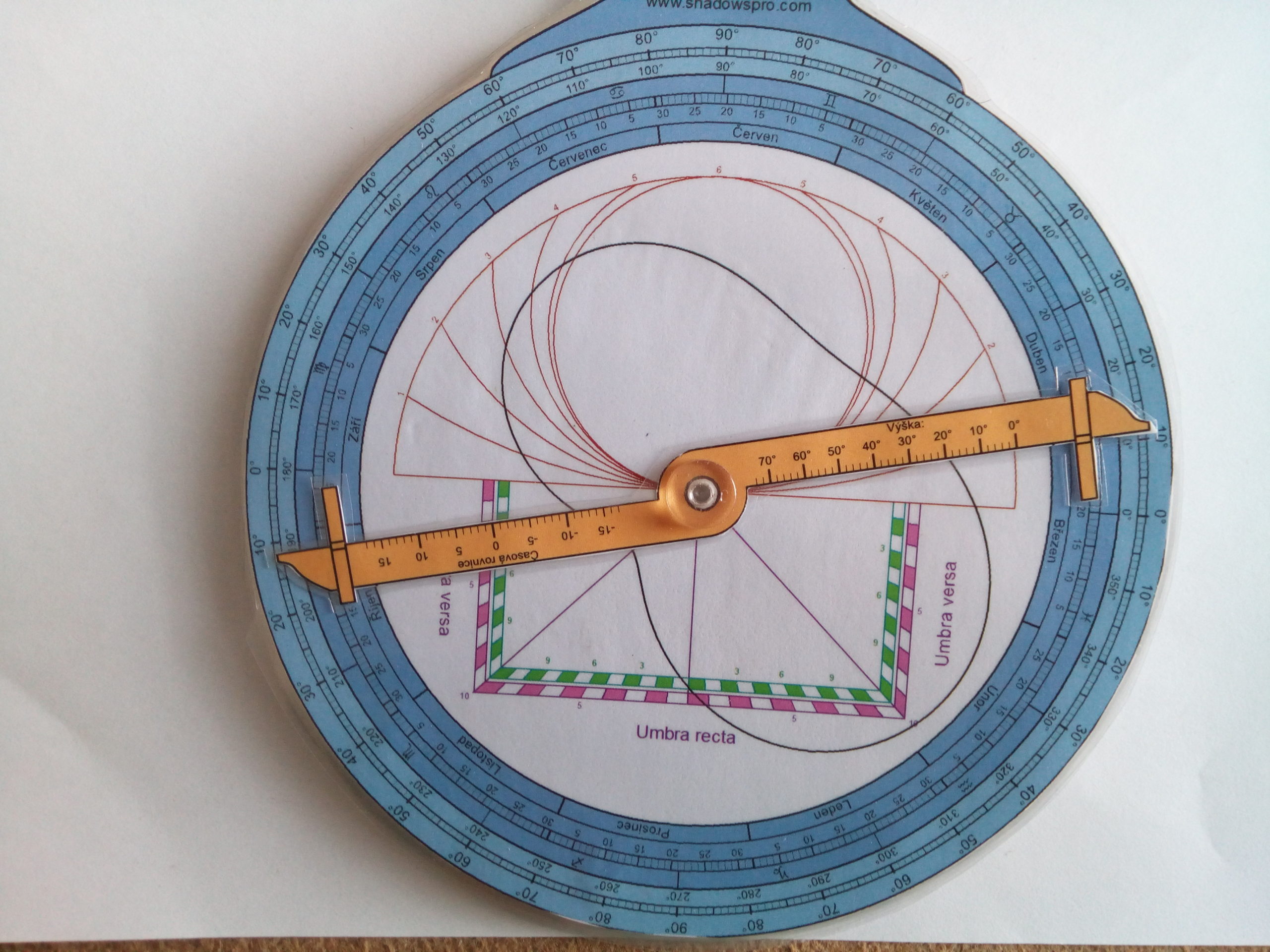
Dále si zjistíme ekliptikální délku pro 9.5. To dává, jak už určitě každý snadno ověří, 49°.
A teď jdeme na přední stranu. Zde natočíme síť tak, aby Vega byla na azimutální kružnici východní 10°. To je kousek vlevo od polední čáry. Pravítko nastavíme na 49° a na časové stupnici čteme 3 hodiny 15 minut, a protože máme letní čas, hodinu přičteme. Výsledek by měl vypadat takto:

8. Určete astrolábem rektascenzi a deklinaci Arktura dne 9.5. 2021, znáte -li jeho výšku nad obzorem ve 20:00 LSEČ.
Tak už víme, jak změřit výšku pomocí alhidády, to bylo v minulém úkolu. Víme, že ekliptikální délka je téměř 49.75°, výška nám vyšla 33°.
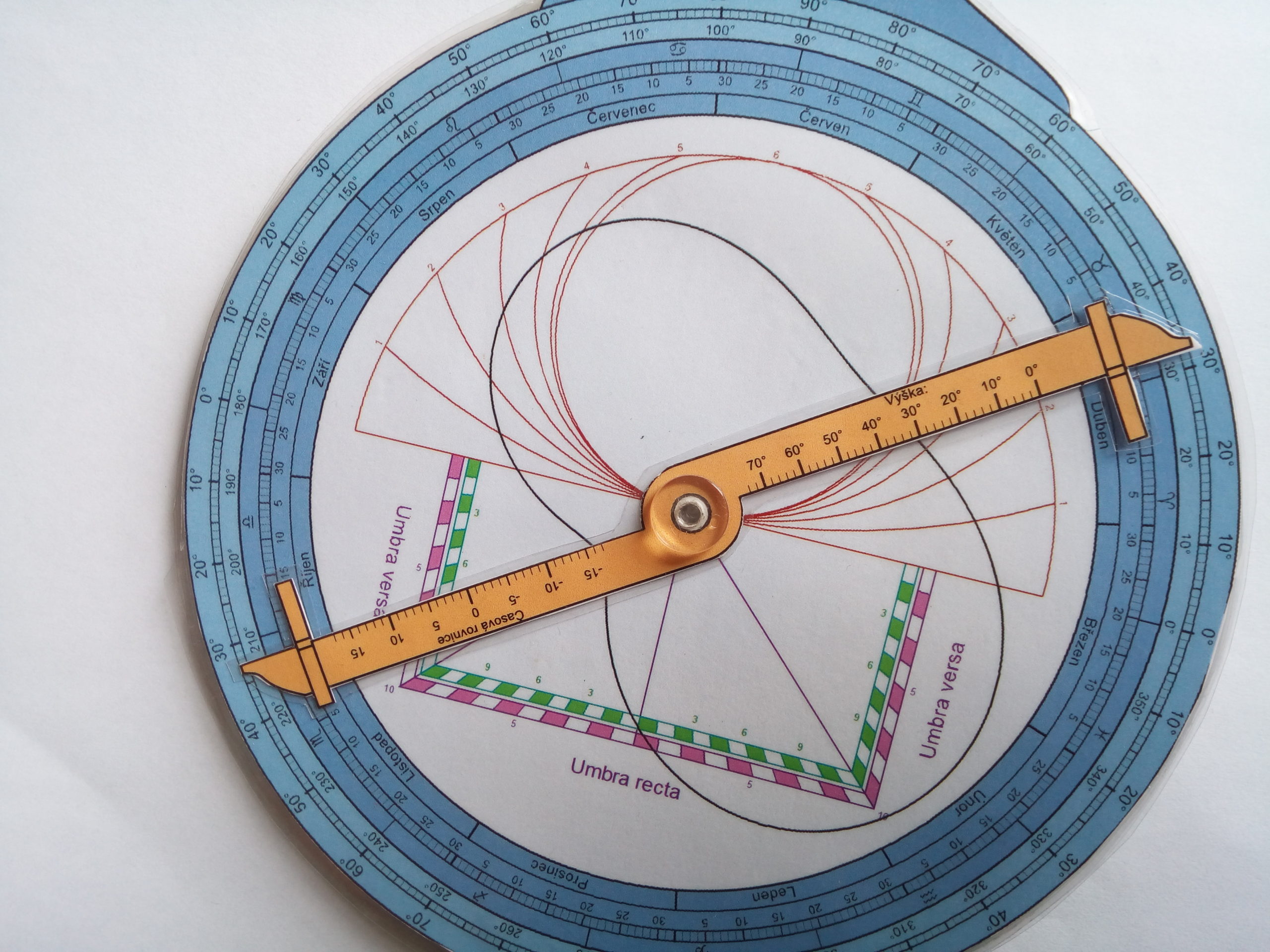
Nyní na přední straně astrolábu nastavíme Arktura na azimutální kružnici 33° vlevo (stále stoupá ke kulminaci). Srovnáme pravítko na hvězdu a na deklinační stupnici čteme 19°. Rektascenzi pak určíme pootočením pravítka na pozici 0° ekliptikální délky a na hodinové škále čteme 0 hodin a 57 minut. Po vynásobení 15 (ale nejprve nutno převést na stupně a jeho desetiny) pak dostáváme ekvivalentní tvar 14° 15´ . Pokud pro kontrolu (abychom demonstrovali užitečnost přístroje) nahlédneme do astromap, dostaneme hodnoty a = 14° 16‘ 39“ a d= 19° 5‘ 39“. To není vůbec špatné. Takto vypadá astroláb v závěru práce:

9. Převeďte do rovníkových souřadnic 2.druhu bod o ekliptikálních souřadnicích 60°délky a 30° šířky.
A tady přichází ke slovu universální astroláb. Konečně se dočkal. Takže pravítko nastavíme zároveň s obzorem. Pak nastavíme brachiolus proti „poledníku“ s hodnotou 60 na pravítku a zároveň 30 na výškové kružnici. Takže takto:
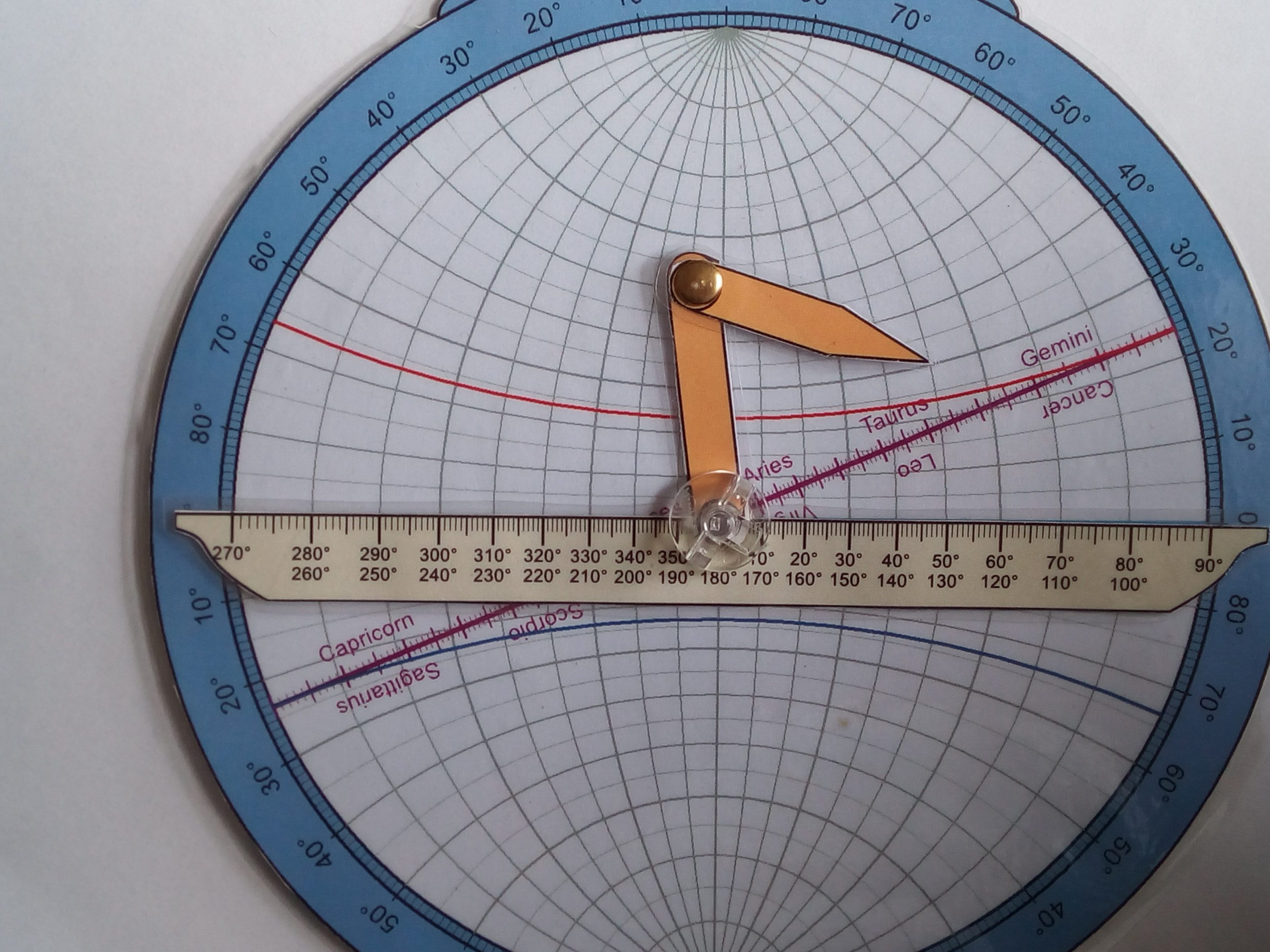
A teď, pokud máte přístroj správně seřízen a opatrným pohybem pravítkem se točí celá ukazatelová soustava, pootočíme pravítkem tak, aby se krylo s rovníkem, to je ta červená čára s vyznačenými znameními. A čteme na konci brachiolu hodnoty rektascenze na poledníkové síti je 48 výšková síť nám určuje 49°deklinace. Viz

Výpočtem můžeme ověřit, že je to přesně 48° 28‘ 47“ a 49° 12‘ 54“. A vzorečky na to nejsou zase tak hezké (i ldyž jsou i mnohem ošklivější), pro ilustraci:
sin (d) = sin (b) * cos (e) + cos (b) * sin (l)
cos (a) = cos (b) * cos (l) / cos (d).
No a teď necháme astroúlohy žít vlastním životem a ukážeme si užití astrolábu k jiným, „přízemnějším“ úlohám. Dnes si představíme něco ze zadní desky, a to sice část, kterou jme v popisku nazvali stínové čtverce. Název mají podle primárního určení, a to je výpočet délky stínu vertikálního gnómonu (část Umbra Recta) či horizontálního gnómonu (Umbra Versa). Spočítáme-li, na kolik dílků je stupnice dělena, dostaneme výšku (délku) gnómonu ve stopách. Nejpoužívanější jsou 7, 9, 10 a 12. A kromě mnoha jiných užití se tyto délky stínů užívaly pro stanovení okamžiků významných modliteb. Například 7 odpovídá muslimskému dni a základnímu dni křesťanskému.
A jak se to používá? No zaměřím Slunce alhidádou a ta mi protne stupnici stínového čtverce. A čtu délku. Například:
10. Jak dlouhý stín vrhne svislý gnómon 10 stop vysoký, jestliže má Slunce výšku 57°?
Jednoduše ověříme, že to dává 6,5 stopy.
11. A jak dlouhý stín ukáže vodorovný gnómon při výšce Slunce 25°?
Tentokrát čteme na druhé(obrácené, Versa) stupnici 5 stop.
Ale tyto čtverce se dají využít i jinak. Ony totiž slouží jako násobící (Recta) či dělící (Versa) koeficienty pro výškoměr. Raději prakticky:
12. Mám strom, jsem od něj 10 metrů daleko, jak je ten strom vysoký?
Změřím pomocí alhidády z 10 metrů, pod jakým úhlem vidím špičku stromu.

Je to stejné, jako u zaměřování hvězd. Nyní mne ale nezajímá hodnota úhlu, ale kde se mi protne alhidáda s vybraným stínovým čtvercem. Na obrázku je 12‘ čtverec.
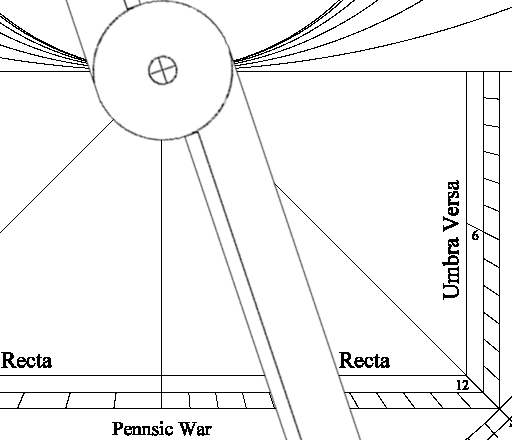
Protože průsečík je v oblasti Recta na hodnotě 4, dostávám 4 /12 = 3 a Recta znamená násobení, tedy 10 (vzdálenost) * 3 = 30 m.
13. A když jsem od věže 200 m, jak ta je vysoká?
Tak opět ze vzdálenosti 200 m zaměřím vrchol věže.
A dostávám na Versa stupnici 3. takže 3 / 12 = 4.
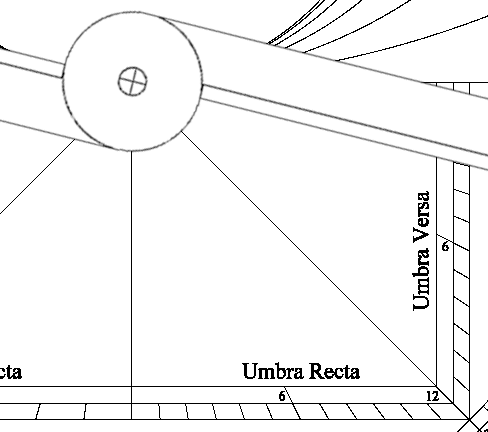
Ale versa znamená dělení, tedy 200 / 4 = 50 m.
Nějaké dotazy?
Ach ano, na obrázcích je to bez jednotek, ale vtip je v tom, že na jednotkách nezáleží. Takže kroky, metry, yardy, stopy … dle libosti.
A taky je to v obou případech špatně, protože já měřím ve výšce očí, ne u země, takže prostě špatně. Je to na nic! NE, není, pochopitelně se přičte ona výška, tedy cca o 15 cm méně, než měřím já. A je to.
Tak pro dnešek zase vše, těším se na příště. Zadní strana astrolábu nabízí, nebo může nabízet daleko víc.
(c) 2021 Hvězdárna v Úpici