
Týden nám utekl a nás čekají další cvičení s kouzelnou lunární volvellou. Tak pozor, jdeme na řešení dvou úloh.
Ta první zní: Jaká je fáze Měsíce dne 18.3.2021 ve 21:00 SEČ? (správná odpověď je první osmina, tj. 4,7 dne stár)
Teď se, milý čtenáři nelekej, pro ilustraci tady uvedu středně přesný výpočet, jak jej uvádějí „chytré knihy“. Abychom následně mohli náležitě ocenit naši LV. Nemusíš to skutečně počítat (ale můžeš). A pokud se Ti, příteli, ze vzorečků dělá špatně, prostě sjeď s textem dolů a čti až za vzorečky.
Pro řešení výše uvedeného zadání je třeba nejprve převést čas na čas světový. To je jednoduché, protože náš čas je pro 15° východní délky, jsme s hodinami vůči 0° o hodinu napřed, takže v UT, jak se světový čas označuje (nebudeme zde teď řešit koordinovanost jiné nadstavby) je to 20:00.
Nyní musíme vypočítat pro zadané datum takzvaný juliánský den JD (nebo juliánské denní číslo či juliánský denní index), což je v astronomických výpočtech jeden z nejzákladnějších údajů.
Zaveďme si pro další potřeby tyto operátory:
+ je sčítání
– je odečítání
* je násobení
/ je dělení
^ je umocňování
\ značí celočíselné dělení (jinak také označované jako dělení se zbytkem, například
13 \ 4 = 3 (zbytek je pak 1)
% značí zbytek po celočíselném dělení, takže 13 % 4 = 1
int () je celočíselná část čísla, tedy to před desetinnou čárkou, např.
int (2,5) = 2.
Označme si den jako D, měsíc jako M a rok jako R. Pak pro M > 2 je vše beze změn a pro M <= 2 platí M = M + 12 a R = R – 1. Nyní vypočítáme pro datum v gregoriánském kalendáři (tedy vše od 15.10.1582 dál do současnosti) opravné koeficienty
A = R \ 100 B = 2 – A + ( A \ 4).
Juliánský den je pak dán vztahem
JD = int (365.25 * R) + int (30,6001 *(M+1)) + D + B + 1720994,5.
Pro data před řehořskou reformou je B = 0.
Teď postoupíme dál, vypočítáme si pomocné číslo
T = (JD – 2415020) / 36525.
Protože toto je jen ilustrační záležitost, nebudeme rozvádět jeho význam, stejně tak i u dalších koeficientů dále, ať tu nudnou matematickou část zbytečně nenatahujeme.
Nyní vypočítáme
d = 350,737486 + 445267,1142*T – 0,001436*(T^2) + 0,0000019*(T^3)
M = 358,475833 + 35999,0498*T – 0,00015*(T^2) – 0,0000033*(T^3)
M’ = 296,104608 + 477198,8491*T + 0,009192*(T^2) + 0,0000144*(T^3)
A jdeme do finále:
i = 180 – d – 6,289*sin(M’) + 2,1*sin(M) – 1,274*sin(2*d – M’) – 0,658*sin(2*d) – 0,214*sin(2*M’) – 0,11*sin(d).
Poměr měsíční plochy osvícené a neosvícené je pak
k = (1 + cos(i)) / 2.
Z tohoto čísla pak ještě musíme vykalkulovat vlastní fázi, tady nám pomůže fakt, že pro
nov je k = 0
první čtvrť k = 0,5
úplněk k = 1
poslední čtvrť k = – 0,5.
Hezký výpočet, že? To dá každý úplně z hlavy. 🙂
No a teď totéž na LV:
Na začátek taky budeme trochu počítat, ale už to bude výrazně kratší a jen jednoduché operace. A navíc bude stačit tento výpočet provést jen jednou.
Takže možná Tě to, milý čtenáři, překvapí, ale existují čísla, která nám říkají, jaká fáze, či přesněji stáří Měsíce je daný den. Tato čísla se souhrnně nazývají epakty. Je jich mnoho druhů, nás ale bude zajímat ta, která se jmenuje gregoriánská epakta. Ta je totiž pro daný rok jedna, říká nám, jak starý Měsíc je 1. ledna daného roku.
A spočteme ji takto:
R je rok, M měsíc a D den, to je jako nahoře.
z = (R % 19) + 1 (pro zájemce o kalendáře – toto je zlaté číslo roku a má zásadní význam v římském kalendáři a pro výpočet Velikonoční neděle)
Ej = (z * 11) % 30 (toto je juliánská epakta)
c = (R \ 100) + 1 (století)
Ks = ((c – 16) * 3) \ 4 (sluneční oprava)
Km = ((c – 15) * 8) \ 25 (měsíční oprava)
Eg = Ej – 10 – Ks + Km (gregoriánská epakta)
Tato epakta pak musí být v rozsahu 0 – 29, takže pokud je větší než 29, musíme odečíst celistvý násobek 30, pokud menší než 0, pak celistvý násobek 30 přičítáme. Takže pro Eg = 38 máme 8, pro Eg = – 2 pak 28 a pro Eg = 61 je to 1.
No a tohle opravdu stačí jen jednou, protože platí, že sousední roky se od sebe liší o 11, tedy jestliže pro letošek je Eg = 16 (můžeš si ověřit), pak pro rok 2020 je to 5 a pro rok příští 27. A tak dále. Stačí si tedy zapamatovat nebo na volvellu tužkou poznamenat Eg pro daný rok a finále je pak už s přesností na 2 dny takhle jednoduché:
Fáze či stáří Měsíce F pro daný den je
F = Eg – 1 + M + D !!!
Takže pro zadané datum nám vychází 16 – 1 + 3 + 18 = 36, tedy výsledek je 36-30 = 6. To docela ujde, chyba je 1,3, když přičteme ještě 0,75 dne (tj. 21:00), pak 2,05 dne.
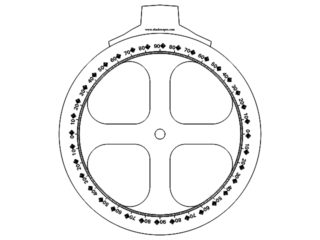
No a teď už stačí jen na volvelle , kalendářní stupnici C, nastavit datum ukazatelem slunečního disku G, ukazatel I měsíčního disku pak nastavíme na odpovídající stáří stupnice H a v okénku J vidíme fázi graficky znázorněnou. A že je tu chyba až 2 dny? No pro řadu lidí v terénu to bohatě stačí, koneckonců okem na obloze rozdíl necvičený pozorovatel skoro nerozezná. A chyba je zpravidla ještě menší. Zrovna letos to je ale opravdu 1,7 dne, tedy skutečný Měsíc byl třeba v lednu téměř o dva dny starší, než jsme vypočítali. Ale to se během roku také změní, vždyť všichni víme, že lunace nejsou stejně dlouhé, oněch 29,5 dne (od novu k novu) je jen průměr. Docela elegantní, co říkáte?
A teď druhá úloha: Kdy bude letos Velikonoční neděle?
Opět nejdřív exaktní výpočet (Spencer – Jonesova modifikace Gaussova algoritmu):
a = R % 19
b = R \ 100
c = R % 100
d = b \ 4
e = b % 4
f = (b + 8) \ 25
g = (b – f + 1) \ 3
h = (19*a + b – d – g + 15) % 30
i = c \ 4
k = c % 4
l = (32 + 2*e + 2*i – h – k) % 7
m = (a + 11*h + 22*l) \ 45
n = (h + l – 7*m + 114) \ 31
p = (h + l – 7*m + 114) % 31
A už to je: n určuje měsíc (3 = březen, 4 = duben), p + 1 pak den.
Na volvelle je to také celkem jednoduché. Fázi už s volvellou umíme, takže si určíme fázi pro 21. březen (dřív to být nemůže, když Velikonoční neděle je ta první po prvním jarním úplňku), zjistíme nejbližší úplněk, pak zjistíme den v týdnu, na který to připadne a odpočítáme následující neděli. Zjednodušit si to můžeme druhým poznamenaným údajem a to jaký den je onen 21.březen. Tím odpadne výpočet dne v týdnu, kde musíme opět počítat juliánský den JD. Pro pořádek:
w = (JD + 1,5) % 7 , 0 = neděle, 1 pondělí …
Ovšem musíme si dávat pozor, touto metodou se můžeme občas o týden splést, jak je tomu právě letos. Protože podle Eg je dle této metody fáze pro 21.3. 2021 rovna 9, je to neděle, do úplňku zbývá 5 – 6 dní, takže úplněk je buď v pátek 26. nebo v sobotu 27.3. Velikonoční neděle je tedy 28.3. A to tedy NENÍ! Je to až o týden později, protože úplněk je ve skutečnosti až v neděli 28.3. To je ta chyba, výše uvedená.
Takže je to na nic? Ale ne, z gregoriánské epakty určíme jednoduše správné datum. Označíme -li si zkratkou PFM index prvního jarního úplňku (z anglického Paschal Full Moon), pak bylo předky pro stanovení PFM odvozeno toto:
Eg je 0 – 23, PFM = 44 – Eg
Eg je 24, PFM = 49
Eg je 25 a zlaté číslo z < 12, PFM = 49 (výpočet z viz výše)
Eg je 25 a z >= 12, PFM = 48
Eg je 26 – 29, PFM = 74 – Eg
Pro PFM < 32 je to březen a PFM dává den úplňku, pro PFM > 31 je to duben a
den je PFM – 31.
Stačí tedy určit den v týdnu, na který to připadá a další neděle je ta pravá. Snadno dopočítáme, že pro letošek nám PFM vychází (pro epaktu 16) rovno 28, takže úplněk je 28. března, což je správně. A protože je to neděle, naše hledané datum je 4.4.2021.
Pokud Vás takovéto jednoduché výpočty zajímají, můžete propátrat internet pro další fígle, a kdo nechce hledat, tak najde třeba tady.
Tak to je pro dnešek vše, bylo to dlouhé, bez obrázků a místy samý nudný vzorec, ale v dalších dílech tomu už tak nebude, toto je jediný bezobrázkový a hodně výpočetní díl. Alespoň ale vidíme, že dávno známé pomůcky a z nich odvozené jednoduché tabulky či pár triviálních výpočtů může posloužit řešení řady celkem složitých úloh. Poslední typické použití LV si ukážeme v následujících dvou dílech, nejprve si ale příště postavíme další přístroj. Ten všichni známe, ale my si jej vyrobíme v trochu rozšířenější verzi a ukážeme si, co včechno lze jednoduše určovat. Tak za týden na sedanou u monitoru.
(c) 2021 Hvězdárna v Úpici